Unit 26: Wildcards

Learning Objectives

Students should

• be aware of the meaning of wildcard ? and bounded wildcards.
• know how to use wildcards to write methods that are more flexible in accepting a range of types.
• know that upper-bounded wildcard is covariant and lower-bounded wildcard is contravariant.
• know the PECS principle and how to apply it.
• be aware that the unbounded wildcard allows us to not use raw types in our programs.

Running Example

For our running example in this unit, we will be using the following subtyping relationship.

abstract class Shape {
    :
}

class Circle extends Shape {
    :
}

class Square extends Shape {
    :
}

class ColoredCircle extends Circle {
    :
}

class LinedCircle extends Circle {
    :
}

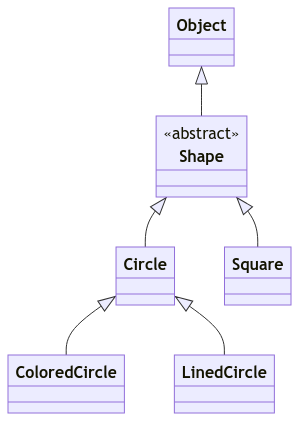
The class diagram for visualization is shown below. Note that Shape extends from Object implicitly.

contains with Array<T>

Now that we have our Array<T> class, let's modify our generic contains method and replace the type of the argument T[] with Array<T>.

Contains with Generic Array<T>Contains with Generic Array T[]

class A {
  // version 0.5 (with generic array)
  public static <T> boolean contains(Array<T> array, T obj) {
    for (int i = 0; i < array.getLength(); i++) {
      T curr = array.get(i);
      if (curr.equals(obj)) {
        return true;
      }
    }
    return false;
  }
}

class A {
  // version 0.5 (with generic array)
  public static <T> boolean contains(T[] array, T obj) {
    for (int i = 0; i < array.length; i++) {
      T curr = array[i];
      if (curr.equals(obj)) {
        return true;
      }
    }
    return false;
  }
}

Similar to the version that takes in T[], using generics allows us to constrain the type of the elements of the array and the object to search for to be the same. This allows the following code to type-check correctly:

Array<String> stringArray;
Array<Circle> circleArray;
Circle circle;
  :
A.<String>contains(stringArray, "hello"); // OK: Array<String> <: Array<String>  &  String <: String
A.<Circle>contains(circleArray, circle);  // OK: Array<Circle> <: Array<Circle>  &  Circle <: Circle

But trying to search for a circle in an array of strings would lead to a type error:

A.<String>contains(stringArray, circle); // ERROR: Circle </: String

Consider now having an array of shapes.

Array<Shape> shapeArray;
Array<Circle> circleArray;
Shape shape;
Circle circle;
  :
A.<Shape>contains(shapeArray, shape);     // OK: Array<Shape>  <: Array<Shape>   &  Shape  <: Shape
A.<Circle>contains(circleArray, circle);  // OK: Array<Circle> <: Array<Circle>  &  Circle <: Circle

As expected, we can pass Shape as the argument for T, and search for a Shape in an instance of Array<Shape>. Similarly, we can pass Circle as the argument for T and search for a Circle in an instance of Array<Circle>.

We could also look for a Circle instance from Array<Shape> if we pass Shape as the argument for T.

A.<Shape>contains(shapeArray, circle); // OK: Array<Shape> <: Array<Shape>   &  Circle <: Shape

Note that we can pass in a Circle instance as a Shape, since Circle <: Shape.

Recall that generics are invariant in Java (i.e., there is no subtyping relationship between Array<Shape> and Array<Circle>). Array<Circle> is not a subtype of Array<Shape>. Otherwise, it would violate the Liskov Substitution Principle, we can put a square into an Array<Shape> instance, but we can't put a square into an Array<Circle> instance.

So, we can't call:

A.<Circle>contains(shapeArray, circle); // ERROR: Array<Shape> </: Array<Circle>

The following would result in compilation errors as well:

A.<Shape>contains(circleArray, shape);  // ERROR: Array<Circle> </: Array<Shape>
A.<Circle>contains(circleArray, shape); // ERROR: Shape </: Circle

Thus, with our current implementation, we can't look for a shape (which may be a circle) in an array of circles, even though this is something reasonable that a programmer might want to do. This constraint is due to the invariance of generics -- while we avoided the possibility of run-time errors by avoiding covariance arrays, our methods have become less general.

Let's see how we can fix this with bounded type parameters first. We can introduce another type parameter, say S, to remove the constraints that the type of the array must be the same as the type of the object to search for. I.e., we change from

  public static <T> boolean contains(Array<T> array, T obj) { .. }

to:

  public static <S,T> boolean contains(Array<T> array, S obj) { .. }

But we don't want to completely decouple T and S, as we want T to be a subtype of S. We can thus make T a bounded type parameter, and write:

  public static <S, T extends S> boolean contains(Array<T> array, S obj) { .. }

Now, we can search for a shape in an array of circles.

     A.<Shape,Circle>contains(circleArray, shape);

Copying to and from Array<T>

Let's consider another example. Let's add two methods copyFrom and copyTo, to Array<T> so that we can copy to and from one array to another.

// version 0.4 (with copy)
class Array<T> {
  private T[] array;

  Array(int size) {
    // The only way we can put an object into the array is through
    // the method set() and we only put an object of type T inside.
    // So it is safe to cast `Object[]` to `T[]`.
    @SuppressWarnings("unchecked")
    T[] a = (T[]) new Object[size];
    this.array = a;
  }

  public void set(int index, T item) {
    this.array[index] = item;
  }

  public T get(int index) {
    return this.array[index];
  }

  public void copyFrom(Array<T> src) {
    int len = Math.min(this.array.length, src.array.length);
    for (int i = 0; i < len; i++) {
      this.set(i, src.get(i));
    }
  }

  public void copyTo(Array<T> dest) {
    int len = Math.min(this.array.length, dest.array.length);
    for (int i = 0; i < len; i++) {
      dest.set(i, this.get(i));
    }
  }
}

With this implementation, we can copy, say, an Array<Circle> to another Array<Circle>, an Array<Shape> to another Array<Shape>, but not an Array<Circle> into an Array<Shape>, even though each circle is a shape!

Array<Circle> circleArray; // T = Circle --> copyTo(Array<Circle>) & copyFrom(Array<Circle>)
Array<Shape> shapeArray;   // T = Shape  --> copyTo(Array<Shape>)  & copyFrom(Array<Shape>)
  :
shapeArray.copyFrom(circleArray); // ERROR: Array<Circle> </: Array<Shape>
circleArray.copyTo(shapeArray);   // ERROR: Array<Shape>  </: Array<Circle>

Upper-Bounded Wildcards

Let's consider the method copyFrom. We should be able to copy from an array of shapes, an array of circles, an array of squares, etc, into an array of shapes. In other words, we should be able to copy from an array of any subtype of shapes into an array of shapes. Is there such a type in Java?

The type that we are looking for is Array<? extends Shape>. This generic type uses the wildcard ?. Just like a wild card in card games, it is a substitute for any type. A wildcard can be bounded. Here, this wildcard is upper-bounded by Shape (i.e., the ? can be substituted with either Shape or any subtype of Shape).

They key here is substituted. Consider our running example. Given the type Array<? extends Shape>, the ? can be substituted with any one of the following:

• Shape: because Shape <: Shape so we get Array<Shape>.
• Circle: because Circle <: Shape so we get Array<Circle>.
• Square: because Square <: Shape so we get Array<Square>.
• ColoredCircle: because ColoredCircle <: Shape so we get Array<ColoredCircle>.
• LinedCircle: because LinedCircle <: Shape so we get Array<LinedCircle>.

This can be seen more clearly by looking at the class diagram. In the class diagram below, the types that can be used to substitute ? is highlighted with red background.

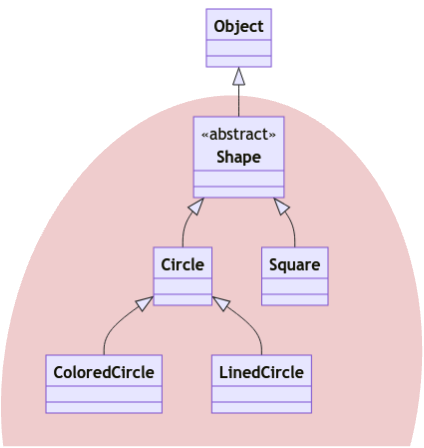
What this means is that we can actually do the following sequence of assignments.

Array<? extends Shape> arr;
arr = new Array<ColoredCircle>(1); // ? is substituted with ColoredCircle
arr = new Array<Square>(1);        // ? is now substituted with Square

The upper-bounded wildcard is an example of covariance. The upper-bounded wildcard has the following subtyping relations:

• If S <: T, then A<? extends S> <: A<? extends T> (covariance)
• For any type S, A<S> <: A<? extends S>

To see this, consider Array<? extends Circle> and Array<? extends Shape>. Now we look at the types that can be used to substitute ? in both cases. The types are summarized in the table below.

Array<? extends Circle>	Array<? extends Shape>
-	Shape
Circle	Circle
-	Square
ColoredCircle	ColoredCircle
LinedCircle	LinedCircle

So, whatever type can be used to substitute ? in Array<? extends Circle> can also be used to substitute ? in Array<? extends Shape>. So the following assignment would work because whatever type we substitute ? with, Array<? extends Shape> can accept those.

Array<? extends Circle> arr1 = ..; // run-time type omitted
Array<? extends Shape> arr2 = arr1;

The table can also be visualized using class diagram. Blue background highlights the type that can be used to substitute ? for Array<? extends Circle> and red background highlights the type that can be used to substitute ? for Array<? extends Shape>. If one is a subset of the other, it implies a subtyping relationship.

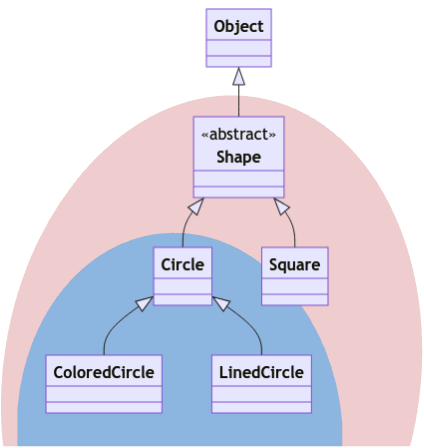
Simply using the covariance rule above, we can also infer a few things. For instance, we can infer Array<Circle> <: Array<? extends Shape>. The proof is as follows

1. Circle <: Shape (given)
2. Array<Circle> <: Array<? extends Circle> (upper-bounded wildcard property)
3. Array<? extends Circle> <: Array<? extends Shape> (using (1) and covariance of upper-bounder wildcard)
4. Array<ircle> <: Array<? extends Shape> (transitivity of subtyping relationship using (2) and (3))

So now, because Array<Circle> <: Array<? extends Shape>, if we change the type of the parameter to copyFrom to Array<? extends T>,

  public void copyFrom(Array<? extends T> src) {
    int len = Math.min(this.array.length, src.array.length);
    for (int i = 0; i < len; i++) {
      this.set(i, src.get(i));
    }
  }

We can now call:

shapeArray.copyFrom(circleArray); // OK: Array<Circle> <: Array<? extends Shape>

without error.

Lower-Bounded Wildcards

Let's now try to allow copying of an Array<Circle> to Array<Shape>.

circleArray.copyTo(shapeArray); 

by doing the same thing:

  public void copyTo(Array<? extends T> dest) {
    int len = Math.min(this.array.length, dest.array.length);
    for (int i = 0; i < len; i++) {
        dest.set(i, this.get(i));
    }
  }

The code above would not compile. We will get the following somewhat cryptic message when we compile with the -Xdiags:verbose flag:

Array.java:32: error: method set in class Array<T> cannot be applied to given types;
        dest.set(i, this.get(i));
          ^
  required: int,CAP#1
  found: int,T
  reason: argument mismatch; T cannot be converted to CAP#1
  where T is a type-variable:
    T extends Object declared in class Array
  where CAP#1 is a fresh type-variable:
    CAP#1 extends T from capture of ? extends T
1 error

CAP?

The type CAP#1 is an internal compiler name for the implicit type parameter represented by the wildcard (i.e., ?). The name comes from "capture". The numbering is to differentiate the different captured types.

Similar to how different declared type parameters are renamed with #1 and #2, all the ? are referring to different implicit type parameters. So, the different ? can be replaced with different type arguments.

Let's try not to understand what the error message means first, and think about what could go wrong if the compiler allows:

        dest.set(i, this.get(i));

Here, we are trying to put an instance with compile-time type T into an array that contains elements with the compile-time type of T or subtype of T.

The copyTo method of Array<Shape> would allow an Array<Circle> as an argument, and we would end up putting instance with compile-time type Shape into Array<Circle>. If all the shapes are circles, we are fine, but there might be other shapes (rectangles, squares) in this instance of Array<Shape>, and we can't fit them into Array<Circle>! Thus, the line

        dest.set(i, this.get(i));

is not type-safe and could lead to ClassCastException during run-time.

Where can we copy our shapes into? We can only copy them safely into an Array<Shape>, Array<Object>, for instance. In other words, into arrays containing Shape or supertype of Shape. Unfortunately our running example no longer have GetAreable. Otherwise, we can also safely insert into Array<GetAreable> too!

We need a wildcard lower-bounded by Shape, and Java's syntax for this is ? super Shape. Using this new notation, we can replace the type for dest with:

  public void copyTo(Array<? super T> dest) {
    int len = Math.min(this.array.length, dest.array.length);
    for (int i = 0; i < len; i++) {
      dest.set(i, this.get(i));
    }
  }

The code would now type-check and compile. We can do the entire reasoning similar to the reasoning we did for upper-bounder wildcard. First, let's keep it specific. We will let T to be Circle. This means Array<? super T> should be treated as Array<? super Circle>¹. So now we try to figure out what are the types that can be used to substitute ? in Array<? super Circle>. There are only 3 possible types:

• Circle: because Circle <: Circle so we get Array<Circle>.
• Shape: because Circle <: Shape so we get Array<Shape>.
• Object: because Circle <: Object so we get Array<Object>.

Again, visually, this will be the following class diagram.

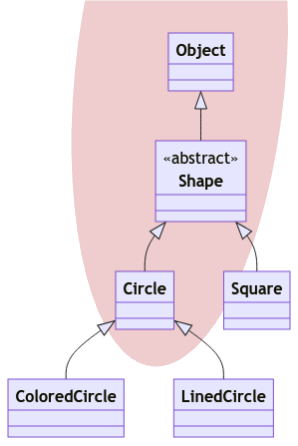
Now, looking back at the relevant part of the code of copyTo, we see the following line:

        dest.set(i, this.get(i));

First, the method set has the following signature: Array::set(int, T). The type T depends on the type of dest. Second, the method get has the following descriptor T Array::get(int). The typeT depends on the type of this.

Now, remember, the compile-time type of dest is Array<? super Circle> and the compile-time type of this is Array<Circle> (because we let T to be Circle). By process of enumeration, we see that all possibilities of types that can be used to substitute ? in the compile-time type of dest can safely accept Circle.

• Circle: the method signature for set is Array::set(int, Circle) and the return type of Array::get(int) is Circle so this type-checked because Circle <: Circle.
• Shape: the method signature for set is Array::set(int, Shape) and the return type of Array::get(int) is Circle so this type-checked because Circle <: Shape.
• Object: the method signature for set is Array::set(int, Object) and the return type of Array::get(int) is Circle so this type-checked because Circle <: Object.

The lower-bounded wildcard is an example of contravariance. We have the following subtyping relations:

• If S <: T, then A<? super T> <: A<? super S> (contravariance)
• For any type S, A<S> <: A<? super S>

Without going into the lengthy explanation with the tables, we will show the class diagram showing that Array<? super Shape> is a subtype of Array<? super Circle>.

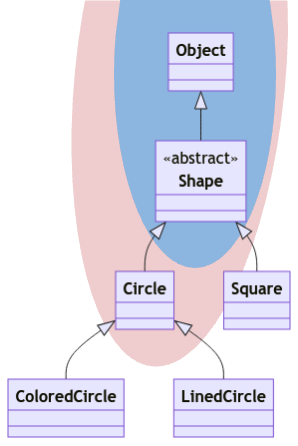
Since we did the proof for upper-bounded wildcard, let us do the same for lower-bounded wildcard. We will show that Array<Shape> <: Array<? super Circle>.

1. Circle <: Shape (given)
2. Array<Shape> <: Array<? super Shape> (lower-bounded wildcard property)
3. Array<? super Shape> <: Array<? super Circle> (using (1) and contravariance of lower-bounded wildcard)
4. Array<Shape> <: Array<? super Circle> (transitivity of subtyping relationship using (2) and (3))

The line of code below now compiles:

circleArray.copyTo(shapeArray); 

Our new Array<T> is now

// version 0.5 (with flexible copy using wildcards)
class Array<T> {
  private T[] array;

  Array(int size) {
  // The only way we can put an object into the array is through
  // the method set() and we only put an object of type T inside.
  // So it is safe to cast `Object[]` to `T[]`.
  @SuppressWarnings("unchecked")
    T[] a = (T[]) new Object[size];
  this.array = a;
  }

  public void set(int index, T item) {
    this.array[index] = item;
  }

  public T get(int index) {
    return this.array[index];
  }

  public void copyFrom(Array<? extends T> src) {
    int len = Math.min(this.array.length, src.array.length);
    for (int i = 0; i < len; i++) {
      this.set(i, src.get(i));
    }
  }

  public void copyTo(Array<? super T> dest) {
    int len = Math.min(this.array.length, dest.array.length);
    for (int i = 0; i < len; i++) {
      dest.set(i, this.get(i));
    }
  }
}

Non Subtype Reasoning

So far, we have shown the visualization for subtyping relationship. In both cases, the types that can be substituted for ? for the subtype is a subset of the types that can be substituted for ? for the supertype. What about the case where there is no subtyping relationship?

Consider Array<? extends Shape> and Array<? super Circle>. Neither are a subtype of the other. So how would this look like in the class diagram?

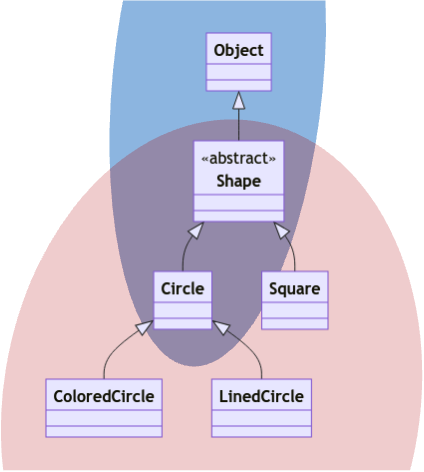
You can see that there is an overlap but clearly, none can be fully contained within the other. This is what it looks like when there is no subtyping relationship.

PECS

Now we will introduce the rule that governs when we should use the upper-bounded wildcard ? extends T and a lower-bounded wildcard ? super T. It depends on the role of the variable. If the variable is a producer that returns a variable of type T, it should be declared with the wildcard ? extends T. Otherwise, if it is a consumer that accepts a variable of type T, it should be declared with the wildcard ? super T.

As an example, the variable src in copyFrom above acts as a producer. It produces a variable of type T. The type parameter for src must be either T or a subtype of T to ensure type safety. So the type for src is Array<? extends T>.

On the other hand, the variable dest in copyTo above acts as a consumer. It consumes a variable of type T. The type parameter of dest must be either T or supertype of T for it to be type-safe. As such, the type for dest is Array<? super T>.

This rule can be remembered with the mnemonic PECS, or "Producer Extends; Consumer Super".

Deriving PECS

While it is easier to simply memorize PECS, you can actually derive these rules yourself. The key here is to change your point of view from the client to the implementer. As a client, you have to think about how you can use the methods implemented by the implementer given the method descriptor. Let's simulate that.

First, a convention. Since we are looking through the lens of a method, the method consumes a value via its parameter. Additionally, the method produces a value via its return value.

Assume that we have the following six variables. We have to exclude Shape because it cannot be instantiated. Note that ColoredCircle <: Circle <: Object.

Object arg1 = new Object();
Circle arg2 = new Circle(..);
ColoredCircle arg3 = new ColoredCircle(..);

Object res1;
Circle res2;
ColoredCircle res3;

Now consider an implementer has implemented the method f with the following descriptor: Circle f(Circle). We can then see which of the method invocation works.

Invocation	Argument Type	Compilation
f(arg1)	Object
f(arg2)	Circle
f(arg3)	ColoredCircle

f(arg1) fails compilation because the parameter is accepting Circle but we are passing Object. Since Object is not a subtype of Circle, we have compilation error.

Now we assume that the argument will always be accepted by the parameter and we look at whether the return type can be accepted by the variable.

Invocation	Variable Type	Compilation
res1 = f(..)	Object
res2 = f(..)	Circle
res3 = f(..)	ColoredCircle

res3 = f(..) fails compilation because the return type is Circle. But we are trying to assign it to ColoredCircle. Since Circle is not a subtype of ColoredCircle, we have compilation error.

Notice how what we have arrived at is the opposite of PECS². Looking at the consumer (i.e., parameter), we actually have "consumer extends" because we can accept Circle or subtype of Circle (e.g., ColoredCircle). Looking at the produced (i.e., return value), we actually have "producer super" because we can accept Circle or supertype of Circle (e.g., Object).

So how do we derive PECS then? We need to look at it from the point of view of the implementer. Consider that as an implementer, you will always do the following line.

res2 = f(arg2);

So now, we need to know which of the following method descriptor can be used for f. Let's draw two tables, one created by varying the parameter type and the other created by varying the return type. Here we have to assume that each method descriptor are compiled separately and there is no overriding and/or overloading.

Method Descriptor	Parameter Type	Compilation
Circle f(Object)	Object
Circle f(Circle)	Circle
Circle f(ColoredCircle)	ColoredCircle

Notice that now we are always passing Circle as argument. So obviously, if a method can accept Object, it can also accept Circle.

Method Descriptor	Return Type	Compilation
Object f(Circle)	Object
Circle f(Circle)	Circle
ColoredCircle f(Circle)	ColoredCircle

Similarly, notice that we are always going to assign the return value to a variable that can accept Circle. So if the method always returns ColoredCircle, it can be assigned to Circle.

The result now conforms to PECS! So to derive PECS, you can change your point of view from client to implementer. This follows the explanation we have given for copyTo and copyFrom. We are -- after all -- the implementer of these two functions. In the case of copyTo, we are always going to invoke the line

        dest.set(i, this.get(i));

This is similar to how we always execute res2 = f(arg2);. Our choice of the type we can use for res2 and arg2 are now restricted. In our derivation here, we change the method descriptor. But in the explanation in this unit, we restrict the type parameter T to behave the way we want it to by using either upper-bounded or lower-bounded wildcards.

Unbounded Wildcards

It is also possible to have unbounded wildcards, such as Array<?>. Array<?> is the supertype of every parameterized type of Array<T>. Recall that Object is the supertype of all reference types. When we want to write a method that takes in a reference type, but we want the method to be flexible enough, we can make the method accept a parameter of type Object. Similarly, Array<?> is useful when you want to write a method that takes in an array of some specific type, and you want the method to be flexible enough to take in an array of any type. For instance, if we have:

void foo(Array<?> array) {
}

We could call it with:

Array<Circle> ac;
Array<String> as;
foo(ac); // ok
foo(as); // ok

A method that takes in generic type with unbounded wildcard would be pretty restrictive, however. Consider this:

void foo(Array<?> array) {
    :
  x = array.get(0);
  array.set(0, y);
}

What should the type of the returned element x be? Since Array<?> is the supertype of all possible Array<T>, the method foo can receive an instance of Array<Circle>, Array<String>, etc. as an argument. The only safe choice for the type of x is Object.

The type for y is every more restrictive. Since there are many possibilities of what type of array it is receiving, we can only put null into array!

There is an important distinction to be made between Array, Array<?> and Array<Object>. Whilst Object is the supertype of all T, it does not follow that Array<Object> is the supertype of all Array<T> due to generics being invariant. Therefore, the following statements will fail to compile:

Array<Object> a1 = new Array<String>(0); 
Array<Object> a2 = new Array<Integer>(0);

Whereas the following statements will compile:

Array<?> a1 = new Array<String>(0);  // Does compile
Array<?> a2 = new Array<Integer>(0); // Does compile

If we have a function

void bar(Array<Object> array) {
}

Then, the method bar is restricted to only takes in an Array<Object> instance as argument.

Array<Circle> ac;
Array<String> as;
bar(ac); // compilation error
bar(as); // compilation error

What about raw types? Suppose we write the method below that accepts a raw type

void qux(Array array) {
}

Then, the method qux is also flexible enough to take in any Array<T> as argument.

Array<Circle> ac;
Array<String> as;
qux(ac); 
qux(as); 

Unlike Array<?>, however, the compiler does not have the information about the type of the component of the array, and cannot type check for us. It is up to the programmer to ensure type safety. For this reason, we must not use raw types.

Intuitively, we can think of Array<?>, Array<Object>, and Array as follows:

• Array<?> is an array of objects of some specific, but unknown type;
• Array<Object> is an array of Object instances, with type checking by the compiler;
• Array is an array of Object instances, without type checking.

Unbounded and Non Wildcard

For completeness, we will show the visualization in class diagram for Array<?> and for non wildcard such as Array<Circle>. In the case of unbounded, it actually encompasses all types!

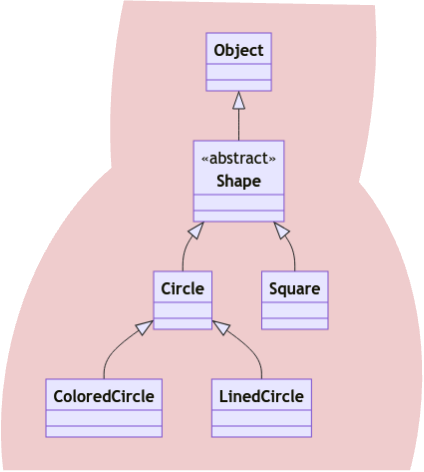
Clearly, it cannot be a subtype of anything besides Array<?> and Object. The latter because Object is the root of the class hierarchy. But at that point, we cannot invoke the methods intended for Array. So while it is more general, it is less flexible to use Object.

Now for non wildcard, it is actually encompasses just that single type. This is why Array<Circle> is a subtype of both Array<? extends Circle> and Array<? super Circle> when we reason only using class diagram visualization.

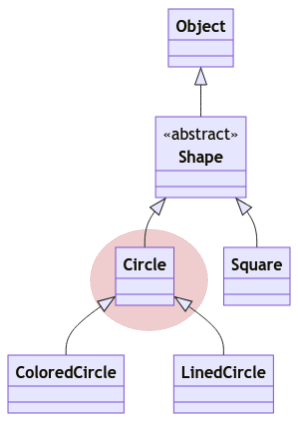
Back to contains

Now, let's simplify our contains methods with the help of wildcards. Recall that to add flexibility into the method parameter and allow us to search for a shape in an array of circles, we have modified our method into the following:

class A {
  // version 0.6 (with generic array)
  public static <S,T extends S> boolean contains(Array<T> array, S obj) {
    for (int i = 0; i < array.getLength(); i++) {
      T curr = array.get(i);
      if (curr.equals(obj)) {
        return true;
      }
    }
    return false;
  }
}

Can we make this simpler using wildcards? Since we want to search for an object of type S in an array of its subtype, we can remove the second parameter type T and change the type of array to Array<? extends S>:

With Wild Cards ArrayWith Generic Array

class A {
  // version 0.7 (with wild cards array)
  public static <S> boolean contains(Array<? extends S> array, S obj) {
    for (int i = 0; i < array.getLength(); i++) {
      S curr = array.get(i);
      if (curr.equals(obj)) {
        return true;
      }
    }
    return false;
  }
}

class A {
  // version 0.6 (with generic array)
  public static <S,T extends S> boolean contains(Array<T> array, S obj) {
    for (int i = 0; i < array.getLength(); i++) {
      T curr = array.get(i);
      if (curr.equals(obj)) {
        return true;
      }
    }
    return false;
  }
}

We can double-check that array is a producer (it produces curr on Line 5) and this follows the PECS rules. Now, we can search for a shape in an array of circles.

     A.<Shape>contains(circleArray, shape);

What is the difference between the two? In version 0.6, we require two type parameters while in version 0.7 we only require one. Say we have both versions in two different classes: A.contains(Array<? extends S>, S) and B.contains(Array<T>, S). Then we have the following behavior:

     A.<Shape>contains(circleArray, shape); // OK
     B.<Shape>contains(circleArray, shape); // ERROR: wrong number of type arguments; required 2

     A.<Shape, Circle>.contains(circleArray, shape); // ERROR: wrong number of type arguments; required 1
     B.<Shape, Circle>.contains(circleArray, shape); // OK

Revisiting Raw Types

In previous units, we said that you may use raw types only in two scenarios. Namely, when using generics and instanceof together, and when creating arrays. However, with unbounded wildcards, we can now see it is possible to remove both of these exceptions. We can now use instanceof in the following way:

a instanceof A<?> 

Recall that in the example above, instanceof checks of the run-time type of a. Previously, we said that we can't check for, say,

a instanceof A<String> 

since the type argument String is not available during run-time due to erasure. Using <?> fits the purpose here because it explicitly communicates to the reader of the code that we are checking that a is an instance of A with some unknown (erased) type parameter.

Similarly, we can create arrays in the following way:

new Comparable<?>[10];

Previously, we said that we could not create an array using the expression new Comparable<String>[10] because generics and arrays do not mix well. Java insists that the array creation expression uses a reifiable type, i.e., a type where no type information is lost during compilation. Unlike Comparable<String>, however, Comparible<?> is reifiable. Since we don't know what is the type of ?, no type information is lost during erasure!

Going forward now in the module, we will not permit the use of raw types in any scenario.

---

1. The reasoning can be made more abstract without restricting T but that will only complicate things and make it more difficult to follow the argument. ↩

2. CEPS? PSCE? ↩